Question

How much heat energy is required to convert 48.3 g of solid ethanol at -114.5 degree C to gasesous ethanol at 135.3 degree C? The molar heat of fusion of ethanol is 4.60 kJ/mol and its molar heat of vaporization is 38.56 kJ/mol. Ethanol has a normal melting point of -114.5 degree C and a normal boiling point of 78.4 degree C. The specific heat capacity of liquid ethanol is 2.45 J/g degree C and that of gaseous ethanol is 1.43 J/g degree

Answer 1

7.21 × 10⁴ J

Step-by-step explanation:

Ethanol is solid below -114.5°c, liquid between -114.5°C and 78.4°C, and gaseous above 78.4°C.

How much heat energy is required to convert 48.3 g of solid ethanol at -114.5°C to gaseous ethanol at 135.3 °C?

We need to calculate the heat required in different stages and then add them.

The moles of ethanol are:

`48.3g.(1mol)/(46.07g) =1.05mol`

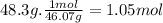
Solid-liquid transition

Q₁ = ΔHfus . n = (4.60 kJ/mol) . 1.05 mol = 4.83 kJ = 4.83 × 10³ J

where,

ΔHfus: molar heat of fusion

n: moles

Liquid: from -114.5°C to 78.4°C

Q₂ = c(l) . m . ΔT = (2.45 J/g.°C) . 48.3g . [78.4°C-(-114.5°C)] = 2.28 × 10⁴ J

where,

c(l): specific heat capacity of the liquid

ΔT: change in the temperature

Liquid-gas transition

Q₃ = ΔHvap . n = (38.56 kJ/mol) . 1.05 mol = 40.5 kJ = 40.5 × 10³ J

where,

ΔHvap: molar heat of vaporization

Gas: from 78.4°C to 135.3°C

Q₄ = c(g) . m . ΔT = (1.43 J/g.°C) . 48.3g . (135.3°C-78.4°C) = 3.93 × 10³ J

where

c(g): specific heat capacity of the gas

Total heat required

Q₁ + Q₂ + Q₃ + Q₄ = 4.83 × 10³ J + 2.28 × 10⁴ J + 40.5 × 10³ J + 3.93 × 10³ J = 7.21 × 10⁴ J