Question

How many lines per mm are there in the diffraction grating if the second order principal maximum for a light of wavelength 536 nm occurs at an angle of 24 degrees with respect to the line from the grating to the center of the diffraction pattern?

Answer 1

To solve this problem it is necessary to apply the concepts related to the principle of superposition and the equations of destructive and constructive interference.

Constructive interference can be defined as

`dSin\theta = m\lambda`

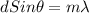
Where

m= Any integer which represent the number of repetition of spectrum

`\lambda`= Wavelength

d = Distance between the slits.

`\theta`= Angle between the difraccion paterns and the source of light

Re-arrange to find the distance between the slits we have,

`d = (m\lambda)/(sin\theta )`

`d = (2*536*10^(-9))/(sin(24))`

`d = 2.63*10^(-6)m`

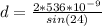
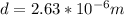
Therefore the number of lines per millimeter would be given as

`(1)/(d) = (1)/(2.63*10^(-6) )`

`(1)/(d) = 379418.5(lines)/(m)((10^(-3)m)/(1 mm))`

`(1)/(d) = 379.4 lines/mm`

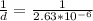
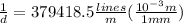
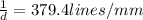
Therefore the number of the lines from the grating to the center of the diffraction pattern are 380lines per mm