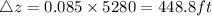Answer:
448.8 ft
Step-by-step explanation:
Area of semi-circle=
![0.5* \frac {pi d^(2)}{4}=\frac {pi* 3^(2){4}* 0.5=3.5325 ft^(2)]()
Hydraulic radius is given by
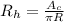 where
where
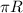 is wetted perimeter,
is wetted perimeter,
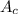 is cross-sectional flow area and
is cross-sectional flow area and
 is hydraulic radius
is hydraulic radius
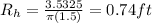
From Manning’s equation, flow rate is given as
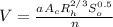
Here,
 is bottom slope,
is bottom slope,
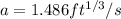
Manning’s coefficient is taken as n=0.014 for open unfinished concrete
Substituting 90 for v, 1.486 for a, 3.5325 for
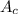 , 0.74 for
, 0.74 for
 and 0.014 for n
and 0.014 for n
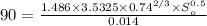
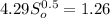
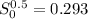
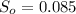
Change in elevation is given by
 where L is distance, here given as 1 mile
where L is distance, here given as 1 mile
1 mile=5280 ft