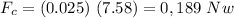Question

In a lab, a 0.025 kg cork attached to a string is swung around in a horizontal circle. The time it takes for the cork to complete one revolution is timed. If the radius of the circle is 0.30 m and one revolution takes 1.25 s, find the speed of the cork and the centripetal force applied to it

Answer 1

v=1.5081 m/s

`F_c=0,189\ Nw`

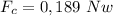
Step-by-step explanation:

Uniform Circular Motion

The cork is performing a circular motion which we assume to be uniform (constant angular speed or angular acceleration zero)

The centripetal force applied to it is given by

`F_c=m\ a_c`

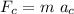
where m is the mass and
`a_c` is the centripetal acceleration. This acceleration appears since the tangent speed is constantly changing direction. If w is the angular speed and r is the radius of rotation

`a_c=w^2r`

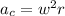
The speed of the cork can be found with the formula

`v=wr`

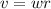
We can compute w since we know the rotation period T=1.25 sec

`w=(2\pi)/(T)=(2\pi)/(1.25)=5.027\ rad/sec`

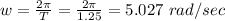
Now, since r=0.30 m, let's compute v

`v=wr=(5.027)(0.3)=1.5081\ m/s`

`a_c=5.027^2(0.3)=7.58\ m/sec^2`

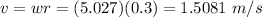
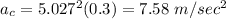
And finally

`F_c=(0.025)\ (7.58)=0,189\ Nw`