Question

a) Γ(n) =∫[infinity]0tn−1e−tdta)Show that Γ(n+ 1) =nΓ(n) using integration by parts.b) Show that Γ(n+ 1) =n! , wherenis a positive integer, by repeatedly applying the result in parta)c) Compute Γ(5).d) Prove what the value of Γ(12) should be by evaluating the gamma function forn= 1/2 and usingthe fact that∫[infinity]0e−u2du=√π2.

Answer 1

`\Gamma(n)=\displaystyle\int_0^\infty t^(n-1)e^(-t)\,\mathrm dt`

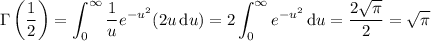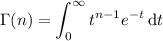
a. Integrate by parts by taking

`u=t^(n-1)\implies\mathrm du=(n-1)t^(n-2)\,\mathrm dt`

`\mathrm dv=e^(-t)\,\mathrm dt\implies v=-e^(-t)`

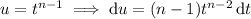
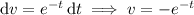
Then

`\displaystyle\Gamma(n)=-t^(n-1)e^(-t)\bigg|_0^\infty+(n-1)\int_0^\infty t^(n-2)e^(-t)\,\mathrm dt`

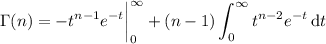
We have

`\displaystyle\lim_(t\to\infty)(t^(n-1))/(e^t)=0`

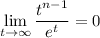
and so

`\Gamma(n)=(n-1)\displaystyle\int_0^\infty t^(n-2)e^(-t)\,\mathrm dt=(n-1)\Gamma(n-1)`

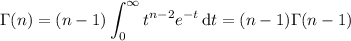
or, replacing
`n\to n+1`,
`\Gamma(n+1)=n\Gamma(n)`.

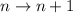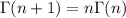b. From the above recursive relation, we find

`\Gamma(n+1)=n\Gamma(n)=n(n-1)\Gamma(n-1)=n(n-1)(n-2)\Gamma(n-2)=\cdots=n(n-1)(n-2)\cdots2\cdot1\Gamma(1)`

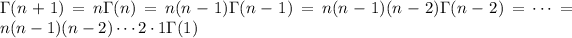
Now,

`\Gamma(1)=\displaystyle\int_0^\infty e^(-t)\,\mathrm dt=1`

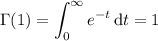
and so we're left with
`\Gamma(n+1)=n!`.

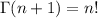c. Using the previous result, we find
`\Gamma(5)=4!=24`.

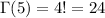d. If the question is asking to find
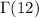`\Gamma(12)`, then you can just use the same approach as in (c).

But if you're supposed to find
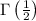`\Gamma\left(\frac12\right)`, we have

`\displaystyle\Gamma\left(\frac12\right)=\int_0^\infty t^(-1/2)e^(-t)\,\mathrm dt`

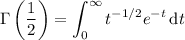
Substitute

`u=t^(1/2)\implies u^2=t\implies 2u\,\mathrm du=\mathrm dt`

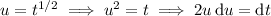
Then

`\displaystyle\Gamma\left(\frac12\right)=\int_0^\infty\frac1ue^(-u^2)(2u\,\mathrm du)=2\int_0^\infty e^(-u^2)\,\mathrm du=\frac{2\sqrt\pi}2=\sqrt\pi`