The worth after 10 years if it were invested at 4% interest compounded continuously is $ 895.094
Solution:
Given that $ 600 invested at 4 % interest compounded continously for 10 years
To find: total amount after 10 years
The compound interest formula for compounded continously is given as:
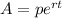
Where "p" is the principal
"r" is the rate of interest
"t" is the number of years
Here in this problem, p = 600

t = 10 years
Substituting the values in formula we get,

Thus the worth after 10 years is $ 895.094