Question

A box slides down a frictionless ramp.if it starts at rest, what is it’s speed at the bottom?

Answer 1

The speed of a box at the bottom of a frictionless ramp can be calculated using the formula v = sqrt(2gh), where g is the gravitational acceleration and h is the height of the ramp.

Step-by-step explanation:

To determine the speed at the bottom of a frictionless ramp when a box starts at rest, we can use the principle of conservation of energy. Since there is no friction to dissipate mechanical energy, the potential energy at the top of the ramp is completely converted into kinetic energy at the bottom. The formula to find the speed v at the bottom is v = sqrt(2gh), where g is the acceleration due to gravity (9.8 m/s2) and h is the height of the ramp.

Assuming we know the height of the ramp, we can simply plug it into the equation to find the speed. The mass of the box is irrelevant in this calculation because it cancels out during the process of converting potential energy to kinetic energy, highlighting that all objects slide down at the same rate on a frictionless incline regardless of their mass.

Answer 2

8.854 m/s is the speed of the box after it reaches bottom of the ramp.

Explanation:

From the figure we came to know that height of the block is 4 m.

We know that,

Total "initial energy of an object" = Total "final energy of an object "

Total "initial energy of an object" is = "sum of potential energy" and "kinetic energy" of an object at its initial position.

`\text {`

`\text { Total initial energy }=\mathrm{m} * \mathrm{g} * \mathrm{h}_{\mathrm{i}}+(1)/(2) \mathrm{m} v_(i)^(2)`

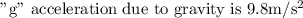
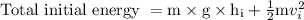
Initial velocity is “0” as the object does not have starting speed

`\text { Height of the block where the object is placed initially }\left(h_(i)\right) \text { is } 4 \mathrm{m} \text { . }`

`\text { Total initial energy }=\mathrm{m} * 9.8 * 4+(1)/(2) \mathrm{m} 0^(2)`

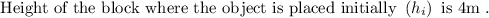
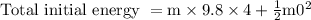
Total initial energy = 39.2 × m

`\text { Total final energy }=\mathrm{m} * \mathrm{g} * \mathrm{h}_{\mathrm{f}}+(1)/(2) m v_(f)^(2)`

`\text { We need to find final velocity } v_f`

`\text { Height of the block where the object is travelled to bottom (h_) is } 0 \mathrm{m} \text { . }`

`\text { Total final energy }=\mathrm{m} * 9.8 * 0+(1)/(2) m v_(f)^(2)`

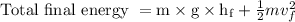
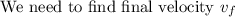
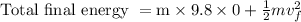
Now, Total initial energy of an object = Total final energy of an object

`39.2 * \mathrm{m}=0.5 \mathrm{m} v_(f)^(2)`

`(39.2)/(0.5)=v_(f)^(2)`

`v_(f)^(2)=78.4`

`v_(f)=√(78.4)`

`v_(f)=8.854 \mathrm{m} / \mathrm{s}`

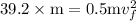
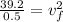
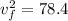
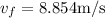
Final speed is 8.854 m/s.