Question

Suppose you spray your sister with water from a garden hose. The water is supplied to the hose at a rate of 0.401 × 10 − 3 m 3 / s and the diameter of the nozzle you hold is 5.27 × 10-3 m. At what speed does the water exit the nozzle?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Flow Rate. It is understood as the volumetric amount transported during a certain time and can be calculated as

`Q = AV`

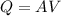
Where

A = Area

V = Velocity

Our values are given as

`r = 5.27*10^(-3)m \rightarrow A = \pi r^2 = \pi ( 5.27*10^(-3))^2 = 8.72*10^(-5)m^2`

`Q = 0.401*10^(-3)m^3/s`

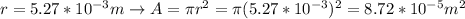
Replacing and rearranging to find the velocity

`V = (Q)/(A)`

`V = (0.401*10^(-3))/(8.72*10^(-5))`

`V= 4.59m/s`

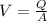
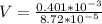
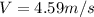
Therefore the speed of the water at the end of the Nozzle is 4.59m/s