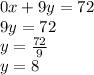Question

What is the value of y in the solution to the system of equations?

One-thirdx + One-fourthy = 1

2x – 3y = –30

A. –8
B. –3
C. 3
D. 8

Answer 1

D

Explanation:

Answer 2

y = 8 (Answer D.)

Explanation:

We need to solve the following system of equations:

`(1)/(3) x+(1)/(4) y=1\\2x-3y=-30`

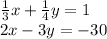
so we start by multiplying both sides of the first equation by 12 so as to get rid of denominators and make our calculations simpler:

`12\,((1)/(3) x+(1)/(4) y)=12\,(1)\\4x+3y=12`

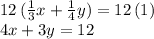
Since we are asked to solve for the unknown "y", we multiply the second equation of the system by "-2", because that way, the term in x will cancel out once we combine both equations term by term:

`(-2)\,(2x-3y)=(-2)\,(-30)\\-4x+6y=60`

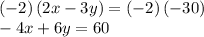
now we combine the two modified equations to solve for the requested unknown "y":

`4x+3y=12\\+\\-4x+6y=60\\---------\\0x+9y=72`

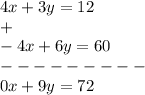
We can now easily solve for y:

`0x+9y=72\\9y=72\\y=(72)/(9) \\y=8`