Question

A simple, harmonic oscillator at the point x=0 generates a wave on a rope. The oscillator operates at a frequency of 40 Hz and with an amplitude of 3.00 cm. The rope has a linear mass density of 50.0 g/m and is stretched with a tension of 5.00 N.

Answer 1

given,

Frequency of oscillator = 40 Hz

Amplitude = 3 cm

linear mass density of rope = 50 x 10⁻³ kg/m

tension = T = 5 N

calculating the speed of wave

`v = \sqrt{(T)/(\mu)}`

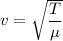
μ is linear mas density of rope

`v = \sqrt{(5)/(50* 10^(-3))}`

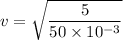
v = 10 m/s

now, calculating the wavelength of the

`\lambda = (v)/(f)`

`\lambda = (10)/(40)`

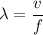
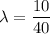
λ = 0.25 m

now calculating transverse acceleration

a = A ω²

ω = 2 π f

ω = 2 π x 40 = 251.32 /m

a = 0.03 x 251.32²

a = 1894.96 m/s²