Question

The DingGnat Doorknob Company intends to sell a new line of square doorknobs. The price-demand function is p ( x ) = 48.5 − 0.09 x p ( x ) = 48.5 - 0.09 x . That is, p ( x ) p ( x ) is the price in dollars at which x x knobs can be sold.

a. How many knobs can be sold at a price of $36.30?

b. Write an equation for the revenue function R(x).

Answer 1

a. 135 doorknobs

b.
`R(x) = 48.5x-0.09 x^2`

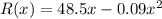
Explanation:

The price-demand function is:

`p(x) = 48.5-0.09 x`

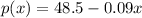
a. At a price of $36.30, the number of doorknobs sold, 'x' is:

`p(x) = 48.5-0.09 x\\36.30 = 48.5-0.09 x\\x= (48.5-36.30)/(0.09)\\x=135.55`

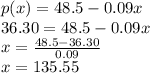
Rounding it down to the nearest whole unit, the company can sell 135 doorknobs at $36.30

b. Revenue is the product of the price, p(x), by the demand, x. Therefore, the Revenue function is:

`R(x) = x*p(x)=x(48.5-0.09 x)\\R(x) = 48.5x-0.09 x^2`