Question

Phonics is an instructional method in which children are taught to connect sounds with letters or groups of letters. A sample of 134 first-graders who were learning English were asked to identify as many letter sounds as possible in a period of one minute. The average number of letter sounds identified was 34.06 with a standard deviation of 23.83.

(a) Construct a 98% confidence interval for the mean number of letter sounds identified in one minute.
(b) If a 95% confidence interval were constructed with these data, would it be wider or narrower than the interval constructed in part a? Explain.
(c) If a sample of 150 students had been studied, would you expect the confidence interval to be wider or narrower than the interval constructed in part (a) ?

Answer 1

98% confidence interval: (29.25,38.87)

Explanation:

We are given the following in the question:

Sample mean,
`\bar{x}` = 34.06

Sample size, n = 134

Sample standard deviation, s = 23.83

a) 98% confidence interval

`\bar{x} \pm z_(critical)\displaystyle(s)/(√(n))`

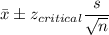
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.02) = \pm 2.33`

`34.06 \pm 2.33((23.83)/(√(133)) ) = 34.06 \pm 4.81 = (29.25,38.87)`

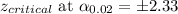
b) If a 95% confidence interval were constructed with these data, confidence interval would be narrower as the confidence level is decreasing as compared to 98%

c) If a sample of 150 students had been studied, the width of confidence interval will decrease as the sample size increases.