Question

You are on a new planet, and are trying to use a simple pendulum to find the gravity experienced on this new planet. You find that a pendulum having a length of 35 cm has a period of 2 seconds. What is the acceleration due to gravity on this planet?

A. 13.82 m/s^2
B. 345.4 m/s^2
C. 3.45 m/s^2
D. 1.1 m/s^2

Answer 1

To solve this problem it is necessary to apply the concepts related to the Period based on the length of its rope and gravity, mathematically it can be expressed as

`T= 2\pi \sqrt{(L)/(g)}`

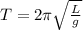
g = Gravity

L = Length

T = Period

Re-arrange to find the gravity we have

`g = (4\pi^2 L)/(T^2)`

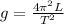
Our values are given as

`L = 0.35m\\T = 2s\\`

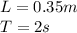
Replacing we have

`g = (4\pi^2 L)/(T^2)`

`g = (4\pi^2 0.35)/(2^2)`

`g = 3.45 m/s^2`

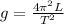
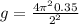
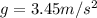
Therefore the correct answer is C.