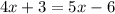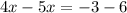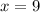Answer:
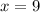
Explanation:
The problem description can be shown in the figure below. Since FG is parallel to BC, both sides AB and AC are split in proportional segments. It can be expressed in several ways. We'll use this one:
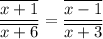
Operating in both sides:

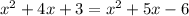
Simplifying