Question

The sodium content of a popular sports drink is listed as 200 mg in a 32-oz bottle. Analysis of 20 bottles indicates a sample mean of 211.5 mg with a sample standard deviation of 18.5 mg.

(a)
State the hypotheses for a two-tailed test of the claimed sodium content.
H0: µ = 200 vs. H1: µ ≠ 200
H0: µ ≥ 200 vs. H1: µ < 200
H0: µ ≤ 200 vs. H1: µ > 200

(b)
Calculate the t test statistic to test the manufacturer’s claim.


(c)
At the 5 percent level of significance (α = 0.05) does the sample contradict the manufacturer’s claim?
__(reject or do not reject)____ H0. The sample _____(contradict or does not contradict)______ the manufacturer's claim.


(d-1)
Use Excel to find the p-value and compare it to the level of significance.
Did you come to the same conclusion as you did in part (c)?

Answer 1

The sample does not contradicts the manufacturer's claim.

Explanation:

We are given the following in the question:

Population mean, μ = 200 mg

Sample mean,
`\bar{x}` = 211.5 mg

Sample size, n = 20

Alpha, α = 0.05

Sample standard deviation, s = 18.5 mg

a) First, we design the null and the alternate hypothesis for a two tailed test

`H_(0): \mu = 200\\H_A: \mu \\eq 200`

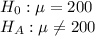
We use Two-tailed t test to perform this hypothesis.

b) Formula:

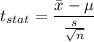`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }` Putting all the values, we have

`t_(stat) = \displaystyle(211.5 - 200)/((18.5)/(√(20)) ) = 2.7799`

c) Now,

`t_(critical) \text{ at 0.05 level of significance, 19 degree of freedom } = \pm 2.0930`

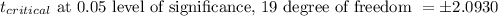
Since, the calculated t-statistic does not lie in the range of the acceptance region(-2.0930,2.0930), we reject the null hypothesis.

Thus, the sample does not contradicts the manufacturer's claim.

d) P-value = 0.011934

Since the p-value is less than the significance level, we reject the null hypothesis and accept the alternate hypothesis.

Yes, both approach the critical value and the p-value approach gave the same results.