Question

Find the length of arc PQ. Round to the nearest tenth.

Answer 1

Answer : The length of arc PQ is, 8.1 in.

Step-by-step explanation :

First we have to calculate the ∠POQ.

As we know that a circle makes an angle of 360° at center.

That means,

∠POQ + ∠QOR + ∠ROS + ∠SOP = 360°

Given:

∠QOR = 65°

∠ROS = 150°

∠SOP = 73°

∠POQ + 65° + 150° + 73° = 360°

∠POQ + 288° = 360°

∠POQ = 360° - 288°

∠POQ = 72°

Now we have to calculate the length of arc PQ.

Formula used :

Length of arc PQ =
`(\theta)/(360^o)* 2\pi r`

where,

`\theta=72^o`

r = radius of circle = 6.48 in

Length of arc PQ =
`(72^o)/(360^o)* 2* 3.14* 6.48in`

Length of arc PQ = 8.1 in

Therefore, the length of arc PQ is, 8.1 in.

Answer 2

The length of arc PQ to the nearest tenth is 8.1 inches.

Explanation:

Let the measure of arc PQ be 'x'.

Given:

The measure of arc SR = 150°

The measure of arc QR = 65°

The measure of arc PS = 73°

Radius of the circle is,
`R=6.48\ in`

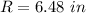
Sum of the measures of all arcs in a circle is always 360°. Therefore,

Arc PQ + Arc QR + Arc SR + Arc PS = 360°

`x+65+150+73=360\\x+288=360\\x=360-288=72\°`

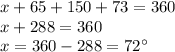
Now, the arc length is given as:

`\textrm{Arc length}=R\theta\\Where\ \theta\rightarrow arc\ measure\ in\ radians`

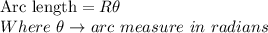
Now, measure of arc PQ,
`\theta=72\°=72* (\pi)/(180)=0.4\pi`

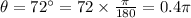
Therefore, arc length PQ =
`6.48* 0.4\pi=2.592* 3.14=8.138\approx 8.1\ in`

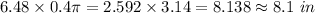
So, the length of arc PQ to the nearest tenth is 8.1 inches.