Question

Suppose a brand of light bulbs is normally​ distributed, with a mean life of 1400 hr and a standard deviation of 150 hr. Find the probability that a light bulb of that brand lasts between 1175 hr and 1610 hr.

Answer 1

The probability that a light bulb of that brand lasts between 1175 hr and 1610 hr is 0.8524.

Explanation:

Given : Suppose a brand of light bulbs is normally​ distributed, with a mean life of 1400 hr and a standard deviation of 150 hr.

To find : The probability that a light bulb of that brand lasts between 1175 hr and 1610 hr ?

Solution :

Applying z-score formula,

`z=(x-\mu)/(\sigma)`

where,
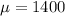`\mu=1400` is population mean

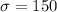`\sigma=150` is standard deviation

For x=1175 hour,

`z=(1175-1400)/(150)`

`z=(-225)/(150)`

`z=-1.5`

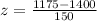
For x=1610 hour,

`z=(1610-1400)/(150)`

`z=(210)/(150)`

`z=1.4`

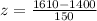
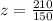
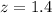
The required probability is,

`P(1175< X<1610)=P(-1.5<z<1.4)`

`P(1175< X<1610)=P(z<1.4)-P(z<-1.5)`

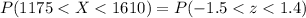
Using z table, the values are

`P(1175< X<1610)=0.9192-0.0668`

`P(1175< X<1610)=0.8524`

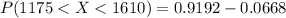
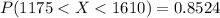
The probability that a light bulb of that brand lasts between 1175 hr and 1610 hr is 0.8524.