Question

A little boy is placing 20 oh his marbles in a row. If 12 are red and 8 are blue and he decides not to place 2 blue marbles next to each other, how many arrangements of the marbles are possible? Expert Answer

Answer 1

Consider lining up all the blue marbles and placing one red marble in between them. Let that arrangement be fixed. The remaining red marbles will be 5 red marbles. Note that the arrangement will be:

x BR x BR x BR x BR x BR x BR x BR x B x

Note that this is the same even if our arrangement is

x B x RB x RB x RB x RB x RB x RB x RB x

Note that there are 9 spots, denoted by x, where we can put the 5 remaining red marbles. To find the number of ways of putting the remaining 5 red marbles to x, it is similar in finding the number of non-negative solution for the equation

`a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + a_9 = 5`

which is given by

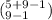`(^(5+9-1)_(9-1))` = 1287

Hence, there are 1287 ways of arranging 8 blue marbles and 12 red marbles without placing 2 blue marbles next to each other.