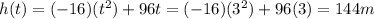Question

Water is launched straight up out of a fountain so that the water droplets return to the ground after about 6 s. What is the initial velocity, in ft/s, of the drops? The height of the water t seconds after launch is modeled by the function: h(t)=-16t^2+96t. What is the maximum height of a drop

Answer 1

The initial velocity is 314.88 ft/s

The maximum height reached is 144 meter.

Explanation:

The total time period is 6 seconds for the raindrop.

Using the equation of motion by differentiating h(t) to give v(t),

`v(t) = -32(t) + 96`

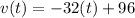
at t=0, v(0) = 96 m/sec = 314.88 ft/sec

It is given that,

`h(t) = (-16)(t^(2)) + 96t`

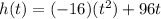
differentiating we get

`v(t) = -32(t) + 96`

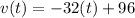
at highest point, v=0;

thus gives us highest point achieved at t=3 seconds.

Height at t=3 seconds is,

`h(t) = (-16)(t^(2)) + 96t =  (-16)(3^(2)) + 96(3) = 144 m`