Answer:
Practical domain:
![v\in[0,230]\ or\ 0\leqslant v\leqslant 230](https://img.qammunity.org/2020/formulas/mathematics/middle-school/uf3yerl947jodozbjjdpl6xwq34h14b0ue.png)
Roger can earn $510 at most when every member of the audience purchases a video
Explanation:
The function
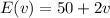
Gives us Roger's earnings when he sells v videos. Knowing the play’s audience consists of 230 people and also each one buys no more than one video, v can take values from 0 to 230 or. equivalently
![v\in[0,230]\ ,\ 0\leqslant v\leqslant 230](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rn8ww80s1flfk4hsyywyuadw4idbculpzt.png)
Those limits become the practical domain of E(v) because if we chose v outside of it, the function would lose validity
If nobody is willing to purchase a video, v=0 and Roger's earings would be
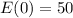
If every person from the audience purchases a video, then v=230 because each person can only purchase 1 video
In that case, where v=230, then
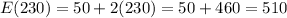
Roger can earn $510 at most.