Answer: b. .8
Explanation:
We find F-test statistic for testing whether two population have equal variances.
As per given , we have
In population 1 .
Samples size :
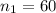
Sample variance :
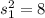
In population 2 .
Samples size :
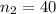
Sample variance :
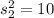
If we want to test whether the variances of the two populations are equal, then the test statistic will have a value of
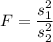
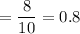
Hence, the value of test-statistic = 0.8
Thus , the correct answer = b. .8