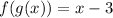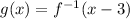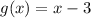Answer:
1)
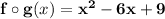 and
and
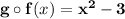 are not equal
are not equal
ie,
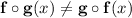
2) The domain is x
Explanation:
Given functions are
 and
and
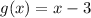
now find the composition of two functions verify that

now find the composition of
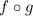

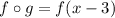
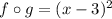
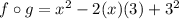

now find the composition of
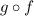

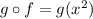
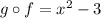
Comparing the above two compositions we get
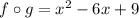 and
and
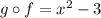 are not equal
are not equal
ie,
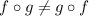 .
.
2) Given that the composition of two function is x-3
Let the functons be f(x) and g(x)
so the composition of two function
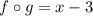
it may be written as