Question

Determine the Reynolds number for a flow of 0.2 m^3/s through a 203 mm inner diameter circular pipe of a fluid with rho=680 kg/m^3 ,μ=3.1*10^(-4) ((N-s)/m^2 ),and σ=0.022 N/m.Is the flow laminar or turbulent?

Answer 1

To find a solution to this problem it is necessary to apply the concepts related to the Reynolds number and its definitions on the type of fluid.

A Reynolds number less than 2000 considers the laminar fluid, while a Reynolds number greater than 4000 is considered a turbulent fluid. (The intermediate between the two values would be a transient fluid)

The mathematical equation that defines the Reynolds number is given by

`Re = (\rho V D)/(\mu)`

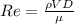
Where

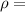`\rho =` Density

V= Velocity

D= Diameter

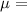`\mu =` Viscosity

Our values are given as

`Q = 0.2m^3/s`

`D = 203*10^(-3)m`

`\rho = 680kg/m^3`

`\mu = 3.1*10^(-4)Ns/m^2`

`\sigma = 0.022N/m`

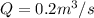
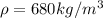
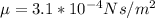
The velocity can be find through the Discharge equation,

Q = VA

Where

V = Velocity

A = Area

Replacing,

`0.2 = V* (2\pi*((203*10^(-3))/(2))^2)`

`V = 3.08m/s`

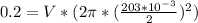
Replacing at the Reynolds equation,

`Re = (\rho VD)/(\mu)`

`Re = (680*3.08*203*10^(-3))/(3.1*10^(-4))`

`Re = 1.37*10^6`

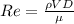
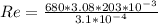
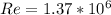
Since Reynolds' number is greater than 4000, then we consider this a turbulent fluid.