Answer:
a)
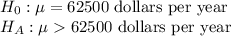
b)
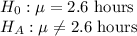
Explanation:
We have to build appropriate null and alternate hypothesis for the given scenarios.
a) Population mean, μ = $62,500 per year
The market research wants to find whether the mean household income of mall shoppers is higher than that of the general population.
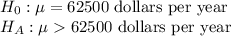
We would use one-tail(right) test to perform this hypothesis.
b) Population mean, μ = 2.6 hours
The company want to know the average time to respond to trouble calls is different or not.
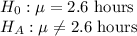
We would use two-tail test to perform this hypothesis.