Question

Two capacitors, a 15 micro F and a 25 micro F, are connected in parallel to a 60 Hz source. The total capacitive reactance is :______

Answer 1

3980.89 ohms

Step-by-step explanation:

The capacitive reactance is expressed as;

`X_c = (1)/(2 \pi fC)`

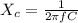
f is the frequency

C is the capacitance of the capacitor

Given

f = 60H

C = C1+C2 (parallel connection)

C = 15μF + 25μF

C = 40μF

C =
`40 * 10^(-6)F`

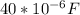
Substitute into the formula:

`X_c = (1)/(2(3.14)*60*40*10^(-6))\\X_c = (1)/(0.0002512)\\X_c = 3,980.89`

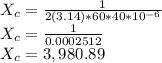
Hence the total capacitive reactance is 3980.89 ohms