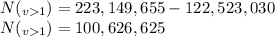Question

How many strings of six lowercase letters of the English alphabet contain

a) exactlyonevowel?
b) exactly two vowels?
c) at least one vowel?
d) at least two vowels?

Answer 1

a) 122,523,030

b) 72,930,375

c) 223,149,655

d) 100,626,625

Explanation:

Consider that there are 5 vowels and 21 consonants in the English alphabet

a) exactly one vowel?

There a 6 possible positions for that vowel (6)

There are 5 ways to choose 1 vowel. (5)

There are 5 other positions to place one of the 21 consonants. (21^5)

`N(_(v=1))=6*5*21^5 = 122,523,030`

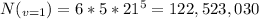
b) exactly two vowels?

There are C(6,2) possible positions for both vowels (C(6,2))

There are 2 positions to choose a vowel out of 5 vowels. (5^2)

There are 4 other positions to place one of the 21 consonants. (21^4)

`N(_(v=2))=C(6,2)*5^2*21^4 = (6!)/((6-2)!2!)*5^2*21^4\\N(_(v=2))= 72,930,375`

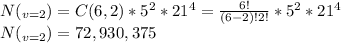
c) at least one vowel?

The number of possibilities that the string contains at least one vowel is the number of total possible outcomes minus the number of outcomes with only consonants:

`N(_(v>0))=(21+5)^6-21^6 \\N(_(v>0))= 223,149,655`

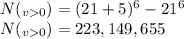
d) at least two vowels?

The number of possibilities that the string contains at least two vowels is the number of possibilities that the string contains at least one vowel minus the number of possibilities that the string contains exactly one vowel:

`N(_(v>1))= 223,149,655 - 122,523,030\\N(_(v>1)) = 100,626,625`