Question

A recent Gallup Poll reported that 86% of 1004 randomly sampled Canadians read at least one book in the past year, compared to 81% of 1009 randomly sampled Britons. Do these results confirm a higher reading rate in Canada? Perform a hypothesis test and state your conclusions.

a. Define the parameters
b. State the hypotheses
c. Define the sampling distribution (mean and standard deviation)
d. Perform the test and calculate P-value
e. State your conclusion
f. Explain what the p-value means in this context

Answer 1

P-value 0.0013 is the probability that the samples drawn from a population where the true proportion of Canadians who read at least one book is not different than the true proportion of Britons who read at least one book in the past year. Assuming a 0.01 significance level, since this probability is low (0.0013<0.01) we can reject the null hypothesis and confirm a higher reading rate in Canada.

Explanation:

let

p(c) be the true proportion of Canadians who read at least one book in the past year, and

p(b) be the true proportion of Britons who read at least one book in the past year

Then, the hypotheses are

`H_(0) : p(c)=p(b)`

`H_(a): p(c)>p(b)`

From the Poll we have two samples. Sampling distributions are:

n1=1004 p1=0.86 mean1=n1×p1=863.44 standard deviation1=
`√(p1*(1-p1))`=
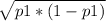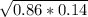`√(0.86*0.14)`≈0.3470

n2=1009 p2=0.81 mean2=n2×p2=817.29 standard deviation2=
`√(p2*(1-p2))`=
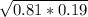`√(0.81*0.19)`≈0.3923

The formula for the test statistic is given as:

z=
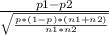`\frac{p1-p2}{\sqrt{(p*(1-p)*(n1+n2))/(n1*n2) } }` where

• p1 is the sample proportion of Canadians who read at least one book in the past year (0.86)

• p2 is the sample proportion of Britons who read at least one book in the past year (0.81)

• p is the pool proportion of p1 and p2 (
  `(n1*p1+n2*p2)/(n1+n2)=0.8349`)

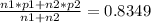• n1 is the sample size of Canadians (1004)

• n2 is the sample size of the Britons (1009)

Then

z=
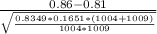`\frac{0.86-0.81}{\sqrt{(0.8349*0.1651*(1004+1009))/(1004*1009) } }` ≈ 3.02

P-value of the test statistic is ≈0.0013.

The probability of the samples drawn from a population where p(c)=p(b) is 0.0013. Assuming a 0.01 significance level, since this probability is low (0.0013<0.01) we can reject the null hypothesis and confirm a higher reading rate in Canada.