Question

Roger is paid $50 to sell videos of a play to an audience after the play is performed.

He also receives $2 for each video he sells. The function E(v)=50+2v
models the amount of money Roger earns by selling v videos. The play’s audience consists of 230 people and each audience member buys no more than 1 video.

What is the practical domain of the function? Show how you determined defined the practical domain. Explain show your process as if you were teaching someone else how to do the work. What is the most that Roger can earn?  help please​

Answer 1

Practical domain:
`v\in[0,230]\ or\ 0\leqslant v\leqslant 230`

Roger can earn $510 at most.

Explanation:

We are given the function

`E(v)=50+2v`

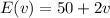
Which gives the earnings of Roger when he sells v videos. Since the play’s audience consists of 230 people and each one buys no more than one video, v can take values from 0 to 230, i.e.

`v\in[0,230]\ or\ 0\leqslant v\leqslant 230`

That is the practical domain of E(v)

If Roger is in bad luck and nobody is willing to purchase a video, v=0

If Roger is in a perfectly lucky night and every person from the audience wants to purchase a video, then v=230. It's the practical upper limit since each person can only purchase 1 video

In the above-mentioned case, where v=230, then

`E(230)=50+2(230)=50+460=510`

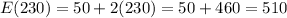
Roger can earn $510 at most.