Question

After once again losing a football game to the college'ss arch rival, the alumni association conducted a survey to see if alumni were in favor of firing the coach. A simple random sample of 100 alumni from the population of all living alumni was taken. Sixty-four of the alumni in the sample were in favor of firing the coach. Let p represent the proportion of all living alumni who favor firing the coach

What is a 90% confidence interval for p? ( upper and lower limit to 4 decimal places)

Suppose the alumni association wished to see if the majority of alumni are in favor of firing the coach. To do this they test the hypotheses H0: p = 0.50 versus Ha: p > 0.50. What is the P-value for this hypothesis test? ( 4 decimal places)

Suppose the alumni association wished to conduct the test at a 1% significance level. What would their decision be? Based on that decision, what type of mistake could they have made?

Answer 1

a) The 90% confidence interval would be given (0.561;0.719).

b)
`p_v =P(z>2.8)=1-P(z<2.8)=0.0026`

c) Using the significance level assumed
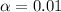`\alpha=0.01` we see that
`p_v<\alpha` so we have enough evidence at this significance level to reject the null hypothesis. And on this case makes sense the claim that the proportion is higher than 0.5 or 50%.

Explanation:

1) Data given and notation

n=100 represent the random sample taken

X=64 represent were in favor of firing the coach

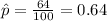`\hat p=(64)/(100)=0.64` estimated proportion for were in favor of firing the coach

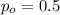`p_o=0.5` is the value that we want to test since the problem says majority

`\alpha` represent the significance level (no given, but is assumed)

z would represent the statistic (variable of interest)

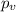`p_v` represent the p value (variable of interest)

p= population proportion of Americans for were in favor of firing the coach

Part a

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

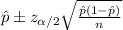
For the 90% confidence interval the value of
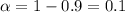`\alpha=1-0.9=0.1` and
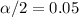`\alpha/2=0.05`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=1.64`

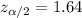
And replacing into the confidence interval formula we got:

`0.64 - 1.64 \sqrt{(0.64(1-0.64))/(100)}=0.561`

`0.64 + 1.64 \sqrt{(0.64(1-0.64))/(100)}=0.719`

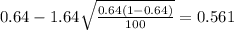
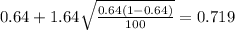
And the 90% confidence interval would be given (0.561;0.719).

Part b

We need to conduct a hypothesis in order to test the claim that the proportion exceeds 50%(Majority). :

Null Hypothesis:
`p \leq 0.5`

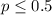
Alternative Hypothesis:
`p >0.5`

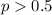
We assume that the proportion follows a normal distribution.

This is a one tail upper test for the proportion of union membership.

The One-Sample Proportion Test is "used to assess whether a population proportion
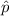`\hat p` is significantly (different,higher or less) from a hypothesized value
`p_o`".

Check for the assumptions that he sample must satisfy in order to apply the test

a)The random sample needs to be representative: On this case the problem no mention about it but we can assume it.

b) The sample needs to be large enough

`np_o =100*0.64=64>10`

`n(1-p_o)=100*(1-0.64)=36>10`

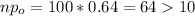
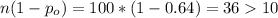
Calculate the statistic

The statistic is calculated with the following formula:

`z=\frac{\hat p -p_o}{\sqrt{(p_o(1-p_o))/(n)}}`

On this case the value of
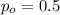`p_o=0.5` is the value that we are testing and n = 100.

`z=\frac{0.64 -0.5}{\sqrt{(0.5(1-0.5))/(100)}}=2.8`

The p value for the test would be:

`p_v =P(z>2.8)=1-P(z<2.8)=0.0026`

Part c

Using the significance level assumed
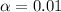`\alpha=0.01` we see that
`p_v<\alpha` so we have enough evidence at this significance level to reject the null hypothesis. And on this case makes sense the claim that the proportion is higher than 0.5 or 50%.