Answer: (15.47, 24.53)
Explanation:
We know that the confidence interval for population mean is given by :_
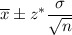
, where n= sample size.
 = standard deviation.
= standard deviation.
 = sample mean.
= sample mean.
z*= Critical value.
Given : n= 450
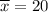
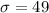
Critical value for 95% confidence = z*=1.96 [From z-value table]
Then, the 95% confidence interval will be :-
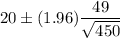
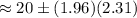
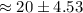
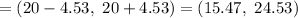
Hence, the 95% confidence interval for the mean change in score μ μ in the population of all high school seniors. : (15.47, 24.53)