Answer:
3.1.1. A(-4, 0) B(0, -2) E(4, 0)
3.1.2. k = -16
3.1.3. (-∞, ∞)
3.1.4. [-16, ∞)
3.1.5. [-6, 4]
Explanation:
Given functions:

Question 3.1.1.
Points A and B are the x-intercept and y-intercept of function h(x).
Point E is the x-intercept of function g(x).
The x-intercept of function h(x) is when h(x) = 0:
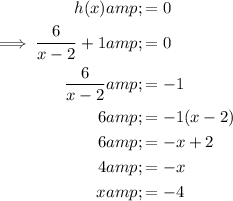
Therefore, the coordinates of point A are (-4, 0).
The y-intercept of function h(x) is when x = 0:
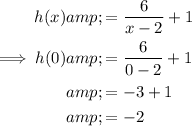
Therefore, the coordinates of point B are (0, -2).
The x-intercept of function g(x) is when g(x) = 0:
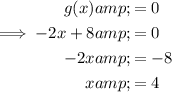
Therefore, the coordinates of point E are (4, 0).
Question 3.1.2.
As function f(x) passes through point C (-6, 20), substitute the point into the equation of the function to find the value of k:
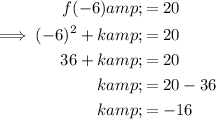
Hence, proving that the value of k is -16.
Question 3.1.3.
The domain is the set of all possible input values (x-values).
The domain of function f(x) is unrestricted, therefore its domain is:
- Solution: -∞ < x < ∞
- Interval notation: (-∞, ∞)
Question 3.1.4.
The range is the set of all possible output values (y-values).
The range of function f(x) is restricted, since the minimum point of the parabola is at (0, -16). Therefore its range is:
- Solution: f(x) ≥ -16
- Interval notation: [-16, ∞)
Question 3.1.5.
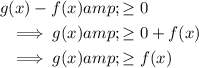
Therefore, find the interval for which g(x) is greater than or equal to f(x).
From inspection of the given graph this is between points C and E:
- Solution: -6 ≤ x ≤ 4
- Interval notation: [-6, 4]