Answer:
396.9 meter
Step-by-step explanation:
If a represents the acceleration,
Then according to the question,
a = -9.8 m/s²,
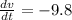 ( acceleration = change in velocity with respect to time ),
( acceleration = change in velocity with respect to time ),
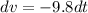
Integrating both sides,
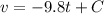
When t = 0 seconds, v = 0 m/s,
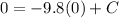

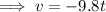
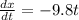 ( velocity = change in position with respect to time ),
( velocity = change in position with respect to time ),
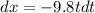
Integrating again,
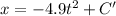
When t = 0 , x = 0 meters,
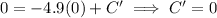
Hence, the final equation that shows the position of the hammer after t seconds,

If t = 9 seconds,
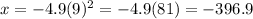 ( negative sign shows the fall ),
( negative sign shows the fall ),
Therefore, it will fall 396.9 meter in 9 seconds