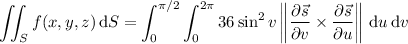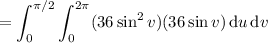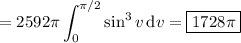You can parameterize
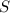 using spherical coordinates by
using spherical coordinates by
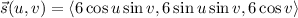
with
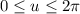 and
and
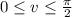 .
.
Take the normal vector to
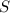 to be
to be
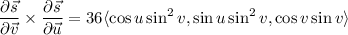
(I use
 to avoid negative signs. The orientation of the normal vector doesn't matter for a scalar surface integral; you could just as easily use
to avoid negative signs. The orientation of the normal vector doesn't matter for a scalar surface integral; you could just as easily use
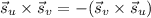 .)
.)
Then
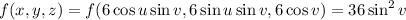
and the integral of
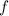 over
over
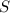 is
is