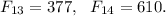Question

Consider the recurrence relation and some initial values for the Fibonacci sequence. Fk = Fk − 1 + Fk − 2 F0 = 1, F1 = 1, F2 = 2, Use the recurrence relation and values for F0, F1, F2, given above to compute F13 and F14.

Answer 1

Answer:
`F_(13)=377,~~F_(14)=610.`

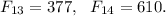
Step-by-step explanation: We are given to consider the following recurrence relation with some initial values for the Fibonacci sequence :

`F_k=F_(k-1)+F_(k-2),~~F_0=1,~F_1=1,~F_2=2.`

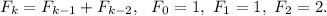
We are given to use the recurrence relation and given initial values to compute
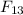`F_(13)` and
`F_(14).`

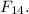
From the given recurrence relation, putting k = 3, 4, . . . , 13, 14, we get

`F_3=F_2+F_1=2+1=3,\\\\F_4=F_3+F_2=3+2=5,\\\\F_5=F_4+F_3=5+3=8,\\\\F_6=F_5+F_4=8+5=13,\\\\F_7=F_6+F_5=13+8=21,\\\\F_8=F_7+F_6=21+13=34,\\\\F_9=F_8+F_7=34+21=55,\\\\F_(10)=F_9+F_8=55+34=89,\\\\F_(11)=F_(10)+F_9=89+55=144,\\\\F_(12)=F_(11)+F_(10)=144+89=233,\\\\F_(13)=F_(12)+F_(11)=233+144=377,\\\\F_(14)=F_(13)+F_(12)=377+233=610.`

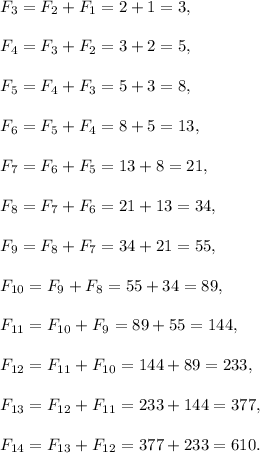
Thus,
`F_(13)=377,~~F_(14)=610.`