Question

The activation energy for a reaction is changed from 184 kJ/mol to 60.5 kJ/mol at 600. K by the introduction of a catalyst. If the uncatalyzed reaction takes about 2537 years to occur, about how long will the catalyzed reaction take? Assume the frequency factor A is constant and assume the initial concentrations are the same.

Answer 1

The catalyzed reaction will take 1,41 s

Step-by-step explanation:

The rate constant for a reaction is:

`k = A e^{-(Ea)/(RT)}`

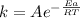
Assuming frequency factor is the same for both reactions (with and without catalyst) it is possible to obtain:

`{(k1)/(k2)} = e^{-(Ea_(2)-Ea_(1))/(RT)}`

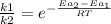
Replacing:

`{(k1)/(k2)} = e^{-(60,5kJ/mol-184kJ/mol)/(8,314472x10^(-3)kJ/molK*600k)}`

`{(k1)/(k2)} = 5,64x10^(10)`

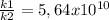
That means the reaction occurs 5,64x10¹⁰ faster than the uncatalyzed reaction, that is 2537 years / 5,64x10¹⁰ = 4,50x10⁻⁸ years. In seconds:

4,50x10⁻⁸ years×
`(365days)/(1year)`×
`(24hours)/(1day)`×
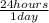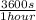`(3600s)/(1hour)` = 1,41 s

I hope it helps!