Question

Identify which of the following statement(s) is always true?

Statement 1: For any positive integer n, the square root of n is irrational.

Statement 2: If n is a positive integer, the square root of n is rational.

Statement 3: If n is a positive integer, the square root of n is rational if and only if n is a perfect square.

Answer 1

Statement 3

Explanation:

Statement 1: For any positive integer n, the square root of n is irrational.

Suppose n = 25 (25 is positive integer), then

`√(n)=√(25)=5`

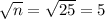
Since 5 is rational number, this statement is false.

Statement 2: If n is a positive integer, the square root of n is rational.

Suppose n = 8 (8 is positive integer), then

`√(n)=√(8)=2√(2)`

Since
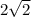`2√(2)` is irrational number, this statement is false.

Statement 3: If n is a positive integer, the square root of n is rational if and only if n is a perfect square.

If n is a positive integer and square root of n is rational, then n is a perfect square.

If n is a positive integer and n is a perfect square, then square root of n is a rational number.

This statement is true.