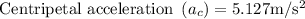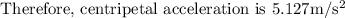Question

A car of mass 1380 kg makes a 19.0 m

radius turn at 9.87 m/s on flat ground.
What is its centripetal acceleration?
(Unit = m/s2)​

Answer 1

5.127

Explanation

Answer 2

`5.127 \mathrm{m} / \mathrm{s}^(2) \text { is the`

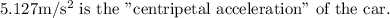
Step-by-step explanation:

Given that,

Mass of the car (m) is 1380 kg

Radius of the car turned (r) is 19.0 m

Speed or velocity of the car (V) is 9.87 m/s

To calculate the “centripetal acceleration” of a car:

`\text { We know that`

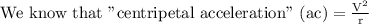
Substitute the given values in the above formula,

`\text { Centripetal acceleration }\left(a_(c)\right)=((9.87 m / s)^(2))/(19 m)`

`\text { Centripetal acceleration }\left(a_(c)\right)=\frac{97.4169 \mathrm{m}^(2) / s^(2)}{19 \mathrm{m}}`

`\text { Centripetal acceleration }\left(a_(c)\right)=5.127 \mathrm{m} / \mathrm{s}^(2)`

`\text { Therefore, centripetal acceleration is } 5.127 \mathrm{m} / \mathrm{s}^(2)`