√(5) * \sqrt[4]{5} ​

Question

`√(5) * \sqrt[4]{5}`
​

Answer 1

Answer: " 3.344 " .

________________________________________

Explanation:

_______________________________________

Note: √5 =
`5^((1/2))` .

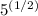→ {Since:
`√(5) = \sqrt[2]{(5^1)}  = \sqrt[2]{5}` } ;

and note the following property of "roots" :

_______________________________________

→
`\sqrt[n]{x^y}  =   x^((y/n))` '

_______________________________________

`\sqrt[4]{5} = 5^((1/4))` .

_______________________________________

→
`√(5)  * \sqrt[4]{5}` ;

=
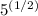`5^((1/2))` * 5^{(1/4) ;

=
`5^([(1/2) +(1/4)])` ;

_______________________________________

Note: Refer to the following property of exponents:

→ xᵃ * xᵇ = x⁽ᵃ ⁺ ᵇ⁾

_______________________________________

Now, (1/2) + (1/4) = ? ;

Note: (1/2) = (?/4) ?? ;

→ Look at the "denominators" ;

2 * ? = 4 ? '

→ 4 ÷ 2 = ? ;

→ 4 ÷ 2 = 2 .

→ So: 2 * 2 = 4; ;

→ Now, look at the "numerators" ;

1 * 2 = 2 ;

So, (1/2) = (2/4) ;

→ (1/2) + (1/4) = (2/4) + (1/4) = (2 + 1) / 4 = 3/4 .

_______________________________________

So:
`5^([(1/2) +(1/4)])` ;

=
`5^(3/4)])` ;

= 3.34370152488 ; (using calculator) ;

→ round to: " 3.344 ".

________________________________________