Answer:
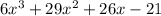
Explanation:
You need to use distributive property and multiply each term of the binomial "3x+7" (that is 3x, and 7) by each term of the trinomial "
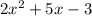 " taking care of their appropriate signs, and then combine like terms until there is no more than one term for each power of "x". It is also customary to order the final terms in descending order of power of "x".
" taking care of their appropriate signs, and then combine like terms until there is no more than one term for each power of "x". It is also customary to order the final terms in descending order of power of "x".
Let's start by multiplying as indicated above:
![(2x^2+5x-3)*(3x+7)=\\=2x^2\,*\,3x+2x^2\,*\,7\,+5x*3x+5x*7-3*3x-3*7=\\=6x^3+14x^2+15x^2+35x-9x-21=\\=6x^3+[14x^2+15x^2]+[35x-9x]-21=\\=6x^3+29x^2+26x-21](https://img.qammunity.org/2020/formulas/mathematics/college/1agbjdmha5r62ydk4a306xzywc4spavmq8.png)