Answer:
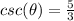
Explanation:
If the
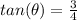 , then the cotangent is
, then the cotangent is
 , given that:
, given that:
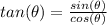 , and
, and
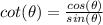 .
.
This is important to know because if you recall the three Pythagorean identities in trigonometry, one of them involves a nice relationship between the cotangent and the cosecant of an angle:
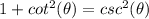
so we can replace
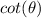 with 4/3, and find what
with 4/3, and find what
 is using that identity:
is using that identity:
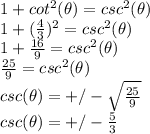
Now, you have to decide on which sign to use. So consider that if the tangent was positive, so most likely you are dealing with an angle
 between 0 and
between 0 and
 , and in that quadrant, the cosecant is positive.
, and in that quadrant, the cosecant is positive.
Therefore, pick the positive value: 5/3