Question

Sec theta - Csc theta / (csc theta)(sec theta)

Answer 1

sin(x)-cos(x)

Explanation:

`((1)/(cos(x)) - (1)/(sin(x))  )/((1)/(sin(x)) * (1)/(cos(x))  )`

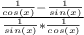
Simplify the denominator:

`((1)/(cos(x)) - (1)/(sin(x))  )/((1)/(cos(x)sin(x))  )`

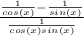
Simplify the numerator:

`\frac{{(2(sin(x)-cos(x)))/(sin(2x)) }  }{(1)/(sin(x)) * (1)/(cos(x))  }`

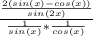
Divide the fractions: (a/b)/(c/d) = (a * d)/(b * c):

`((-cos(x)+sin(x))*2cos(x)sin(x))/(sin(2x))`

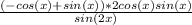
Use the identity: 2cos(x)sin(x) = sin(2x):

`(sin(2x)(-cos(x)+sin(x)))/(sin(2x))`

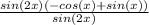
Cancel out the common factor (sin(2x)):

-cos(x) + sin(x)

Simplify:

sin(x) - cos(x)