Answer:
A dashed straight line has a positive slope and goes through (0, negative 4) and (3, negative 2). Everything to the right of the line is shaded.
Explanation:
To graph the solution set of the inequality 2x - 3y < 12, first plot the dashed line 2x - 3y = 12 (dashed because the inequality has sign < without notion "or equal to"). This line passes through the points (0,-4) and (3,-2) (their coordinates satisfy the equation of the line). this line has positive slope because
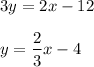
and the slope of the line is 2/3.
Now, identify where the origin is (in the region or outside the region). Substitute (0,0) into the inequality:
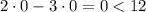
This means coordinates of the origin satisfy the inequality, so origin belongs to the shaded region. Thus, shade that part which contains origin.