Answer:
The quantity of 40 % solution is 4 liters and
The quantity of 60 % solution is 4 liters .
Explanation:
Given as
A pharmacist has 40% and 60% iodine solutions on hand.
Let the quantity of 40 % iodine solutions = x liter
And The quantity of 60 % iodine solutions = y liter
The total quantity of iodine mixture = 8 liter
I.e The quantity of 40 % iodine solutions + the quantity of 60 % iodine solutions = 8 Liter
or x + y = 8
The The percentage of mixture solution = 50 %
∴ 40 % of x + 60 % of y = 50 % of 8
I.e 40 x + 60 y = 400 ..........A
And x + y = 8
Or, 40× ( x + y ) = 40× 8
or, 40 x + 40 y = 320 ...........B
Now , solving equations A and B
I.e ( 40 x + 60 y ) - ( 40 x + 40 y ) = 400 - 320
Or, ( 40 x - 40 x ) + ( 60 y - 40 y ) = 80
Or, 0 + 20 y = 80
∴ y =
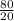
I.e y = 4 liters
So, The quantity of 60 % iodine solution = y = 4 liters
Put The value of y in Eq A
So , 40 x + 60 × 4 = 400
Or, 40 x = 400 - 240
or, 40 x = 160
∴ x =

I.e x = 4 liter
So, The quantity of 40 % iodine solution = x = 4 liters
Hence The quantity of 40 % solution is 4 liters and the quantity of 60 % solution is 4 liters . Answer