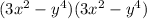Question

How to factor 9x^4-6x^2y^4+y^89x4−6x2y4+y8

Answer 1

`(3x^2-y^4)(3x^2-y^4)`

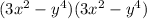
Explanation:

We'll assume the correct expression to be factored is

`9x^4-6x^2y^4+y^8`

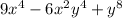
One must try to find out if the expression is a perfect square. To test it, we'll take the square root of the first and the last term. If they are exact, we'll procceed with the next step

`√(9x^4)=3x^2`

`√(y^8)=y^4`

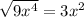
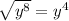
Since both are exact, we'll test if the middle term is twice the product of both square roots:

`2(3x^2)(y^4)=6x^2y^4`

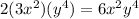
We confirm the middle term equals the above expression. All tests confirm the original expression is

`\left ( 3x^2-y^4 \right )^2`

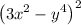
The required factoring is

`(3x^2-y^4)(3x^2-y^4)`