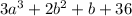Question

2(a³+b²+11)+1(3+a³+b+11)

Answer 1

`2(a^3+b^2+11)+1(3+a^3+b+11)=3a^3+2b^2+b+36`

Explanation:

I assume that you need simplification of the given expression.

The given expression is:

`2(a^3+b^2+11)+1(3+a^3+b+11)`

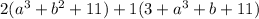
Using distributive property and multiplying 2 inside the parenthesis and 1 inside the other parenthesis. This gives,

`2(a^3+b^2+11)=2* a^3+2* b^2+2* 11\\2(a^3+b^2+11)=2a^3+2b^2+22\\\\1(3+a^3+b+11)=1* 3+1* a^3+1* b+1* 11\\1(3+a^3+b+11)=3+a^3+b+11=a^3+b+14`

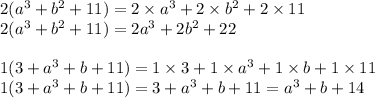
Therefore,
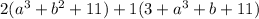`2(a^3+b^2+11)+1(3+a^3+b+11)` is equal to:

`2a^3+2b^2+22+a^3+b+14`

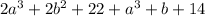
Now, combining like terms using the commutative property of addition, we get:

`=(2a^3+a^3)+2b^2+b+(22+14)\\=3a^3+2b^2+b+36`

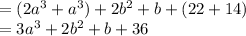
Therefore, the simplified form is
`3a^3+2b^2+b+36`