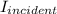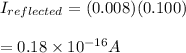Answer:
Step-by-step explanation:
The reflection coefficient is the ratio of reflected flux to the incident flux
The reflection coefficient of a srep potential when a particle is
 is incident on the barrier is given as:
is incident on the barrier is given as:
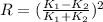
Where
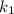 is the propagation constant of the incident wave and
is the propagation constant of the incident wave and
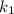 is the propagation constant of transmitted wave.
is the propagation constant of transmitted wave.
The expression for the
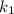 is given as:
is given as:
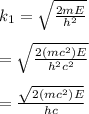
Here
 is the electron mass;
is the electron mass;
 the reduced plancks constant;
the reduced plancks constant;
 the speed of light and
the speed of light and
 the energy of the incident wave.
the energy of the incident wave.
substituting
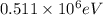 for
for
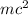 ;
;
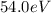 for
for
 and
and
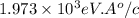 for
for
 in the equation
in the equation
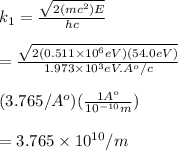 this is the propagation constant for the incident wave.
this is the propagation constant for the incident wave.
For

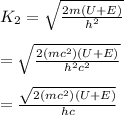
Here
 is the electron mass;
is the electron mass;
 the reduced plancks constant;
the reduced plancks constant;
 the speed of light and
the speed of light and
 the energy of the incident wave.
the energy of the incident wave.
substituting
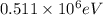 for
for
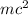 ;
;
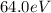 for
for
 and
and
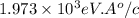 for
for
 in the equation
in the equation
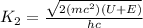
 this is the propagation constant for the transmitted wave.
this is the propagation constant for the transmitted wave.
substituting
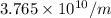 for
for
 and
and
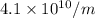


The ratio of the reflected current to the incident current is the reflection coefficient.
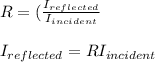
substituting 0.0018 for R and 0.100mA for