Question

A helicopter flies 250 km on a straight path in a direction 60° south of east. The east component of the helicopter's

displacement is
km.

Answer 1

Displacement- 125km

Step-by-step explanation:

EDGE

Answer 2

The east component of the helicopter's displacement is 125 km.

Step-by-step explanation:

Given:

The magnitude of displacement is,
`S=250\ km`

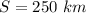
The direction of displacement is 60° south of east.

The direction is shown in the figure below. From the figure, the horizontal component of the displacement vector is the east component.

Thus, the east component of displacement is given as:

`S_(x)=S\cos 60\°\\S_x=250* (1)/(2)=125\ km`

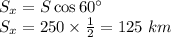
Hence, the east component of the helicopter's displacement is 125 km.