Question

NJCU uses thousands of BrightLight fluorescent light bulbs each year. A new manufacturer, LightLight, claims that its new brand of bulbs, which cost the same as the brand NJCU currently uses, has a mean life of 6000 hours. The university has never studied how long BrightLight bulbs last and they decided they’re curious to see how long LightLight bulbs last compared to LightLight bulbs. NJCU decides to conduct a significance test at the .05 significance level. 64 Bright Light bulbs are tested and the mean life time is found to be 5910 hours. Both manufacturers report that the standard deviation for the lifespan of light is 400 hours.

What is the type, mean and standard deviation of the sampling distribution under the null hypothesis?

What is the value of the sample mean?

Answer 1

N(6000,75) as per H0

Explanation:

Given that NJCU uses thousands of BrightLight fluorescent light bulbs each year. A new manufacturer, LightLight, claims that its new brand of bulbs, which cost the same as the brand NJCU currently uses, has a mean life of 6000 hours.

Sample test of 64 bulbs gave mean as 5910 and std deviation as 600 hours

As per central limit theorem, since sample size is 64 is sufficiently large we can say that sample mean follows a normal distribution

The mean would be 6000 and std deviation of sample would be

`(s)/(√(n) ) \\=(600)/(√(64) ) \\=75`

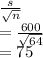
Thus we find x bar would be N(6000,75) as per H0

Value of sample mean = 5910