Answer:
A. 32, 85, 89, 91, 92, 92
Explanation:
A. 32, 85, 89, 91, 92, 92
Mean
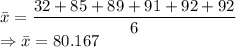
Since the number of scores is 6 which is an even number the median will be of the form
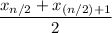
Median
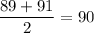
Difference of mean and median =
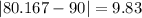
B. 72, 78, 79, 80, 82, 82
Mean
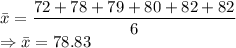
Median
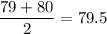
Difference of mean and median =
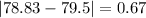
C. 65, 70, 75, 80, 85, 90
Mean
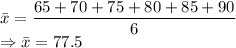
Median
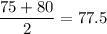
Difference of mean and median =
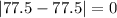
D. 30, 34, 39, 41, 48, 50
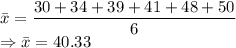
Median
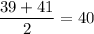
Difference of mean and median =
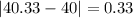
So, A has the maximum difference of 9.83 between the mean and the median.