Question

7597.7 feet

7428.9 feet

10468 feet

• The western border of the farmland is 7597.7 feet.

• The eastern border of the farmland is 7428.9 feet.

• The southern border of the farmland is 10468 feet.

• The farmer will pay $6,500 per square mile of trees removed.

Estimate the cost, in dollars, the farmer will pay to have the trees removed from

the farmland.

Answer 1

`\$18,330`

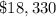
Explanation:

1) Usually, the areas of farms, properties, etc. are quadrilateral forms. Since these legs are not congruent and there's one leg missing then the farmland consists of a trapezoid. Finding out the northern border.

`[tex]BD^(2)=AD^(2)+AB^(2)\Rightarrow BD=\sqrt{7597.7^(2)+10468^(2)}\Rightarrow BD=\pm 12,934.60 \: ft\\BD^(2)=BC^(2)+CD^(2)\Rightarrow 12934.60^(2)=7428.9^(2)+CD^(2)\Rightarrow CD=10588.45`

2)Tracing a line segment connecting BD, and since AD ⊥ BD we have two right triangles. So now let's calculate the hypotenuse and subsequently, the northern leg of this trapezoid, to finally calculate the area. Notice that, we flipped the figure and took the southern border as the height.

`\\S\:farmland=(1)/(2)(7597.7+7428.9)10468\Rightarrow S=78659224.4 ft^(2)`

3) Finally, converting from square feet to a square mile. Knowing that 1 square foot is equal to 3.59 square mile. And multiplying the converted outcome in square miles by $6500 the cost for the farmer is $18,330.

`1 square\:feet = 3.59\:square\:mile\:S =2.82\:mi^(2)\\If \: 1 \:mi^(^2)=\$6,500\:\:then \:3.59\:mi^(2)\:=\$18,330`